Деление в Мумиматике - пожалуй самая сложная из наших тем, но это в любой математике так - хоть бы и в человеческой. В Мумиматике есть, тем не менее, существенное преимущество - наше деление прощает небольшие промахи (но не ошибки) и позволяет вам двигаться в вашем темпе.
Начнем с обычного, человеческого деления - вот как оно выглядит на простом примере: 2603 / 137
Запишем числа:
Начнем с единицы:
Вычтем и получим остаток:
Сносим следующую цифру вниз:
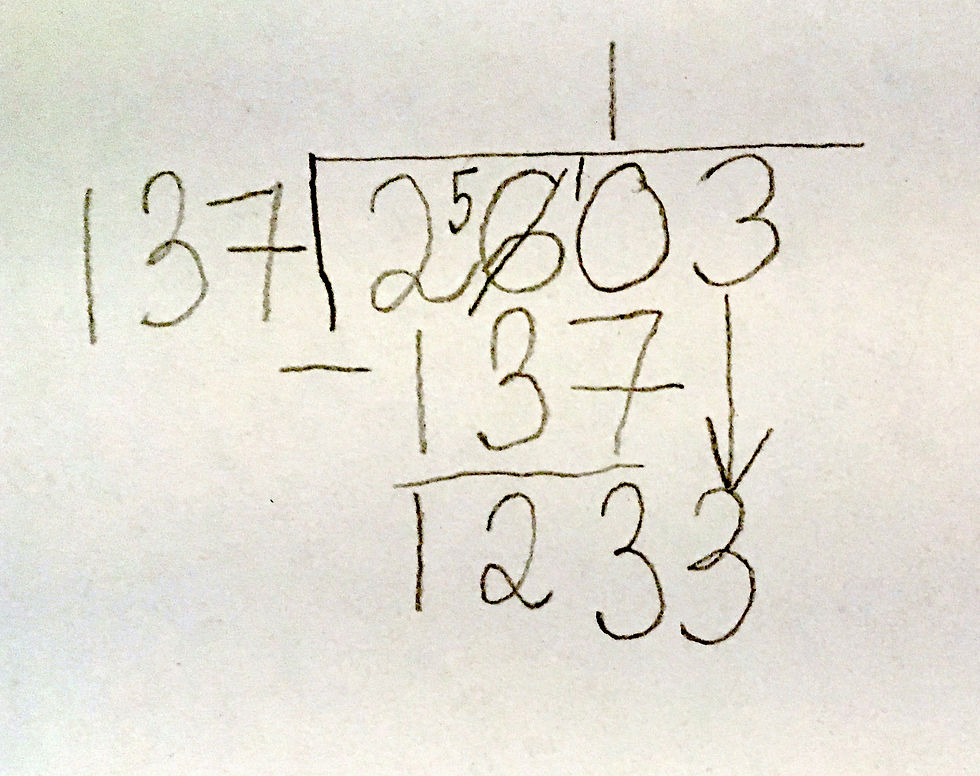
Теперь как-то все непросто, придется умножать отдельно, но, кажется, восьмерка должна подойти:
Пробуем:
Ох нет, не подходит, должно быть - девять:
Да, девять подходит идеально, наш ответ - 19
Мумиматика не требует точно подбирать число на каждом шаге и не ограничивает вас в числе шагов. Вот смотрите - записываем наши числа (делитель и делимое, в этом порядке):
Почему бы ни начать с дюжины? На нее легко умножать - такая причина ничем не хуже любой другой.
Умножим делимое на дюжину, это совсем легко:
Вычтем результат из делимого: складывать и вычитать в Мумиматике - одно удовольствие, ответ буквально виден невооруженным глазом:
Возьмем теперь полдюжины. Кажется, пойдет, и тоже легко умножать:
Вычтем из остатка:
Вот и все, у нас осталась единица:
Нужно только собрать вместе наш ответ - дюжина, полдюжины и единица:
Шагов получилось три, но могло быть и больше и меньше - деление в Мумиматике штука гибкая и нетребовательная, а результат предсказуемо тот же: 12 + 6 + 1 = 19
Задание:
Попробуйте просто повторить наше деление, не подглядывая в решение наверху. И не обязательно в точности: попробуйте, например, маленькие шажки - по полдюжины каждый раз - Мумиматическое деление позволяет вам двигаться в своем темпе.
В следующей лекции - разоблачения и признания. Мумиматику мы сконструировали из разных математик, которыми люди пользовались в разных странах и в разные времена (и немножко добавили своего). Мы расскажем, что и откуда мы взяли, и объясним - почему.